多項分類
評価指標
多項分類とよく似た 二項分類 について既にある程度議論を行ったので、ここでは違いに注目したいと思います。一番の違いは、結果がちょうど二つなのではなく、三つ以上あることです。
結果の全てが等しく興味深いもので、それらのうちいずれも特別強調されるものではないと仮定すると、評価指標に Accuracy(正解率) を選択することが理にかなっており、 正解率が最も高いモデルが好まれます。
N 個の結果があるとき、混同行列は N x N の要素をもっています。正しい予測は対角線上にあり、間違った予測は対角線外にあります。 モデルの比較 でのパフォーマンステーブルでは、 正解率 と Classification Error(分類エラー)のみ表示され、 Precision(適合率) や Recall(再現率) に似たものを、各モデルの Performance(パフォーマンス) タブで確認できます。 適合率 は各行で計算され、 再現率 は各列で計算されます。
| 実際には A | 実際には B | 実際には C | Precision(適合率) | |
|---|---|---|---|---|
| 予測は A | 真に A | 真に A / 予測は A | ||
| 予測は B | 真に B | 真に B / 予測は B | ||
| 予測は C | 真に C | 真に C / 予測は C | ||
| Recall(再現率) | 真に A / 実際には A | 真に B / 実際には B | 真に C / 実際には C |
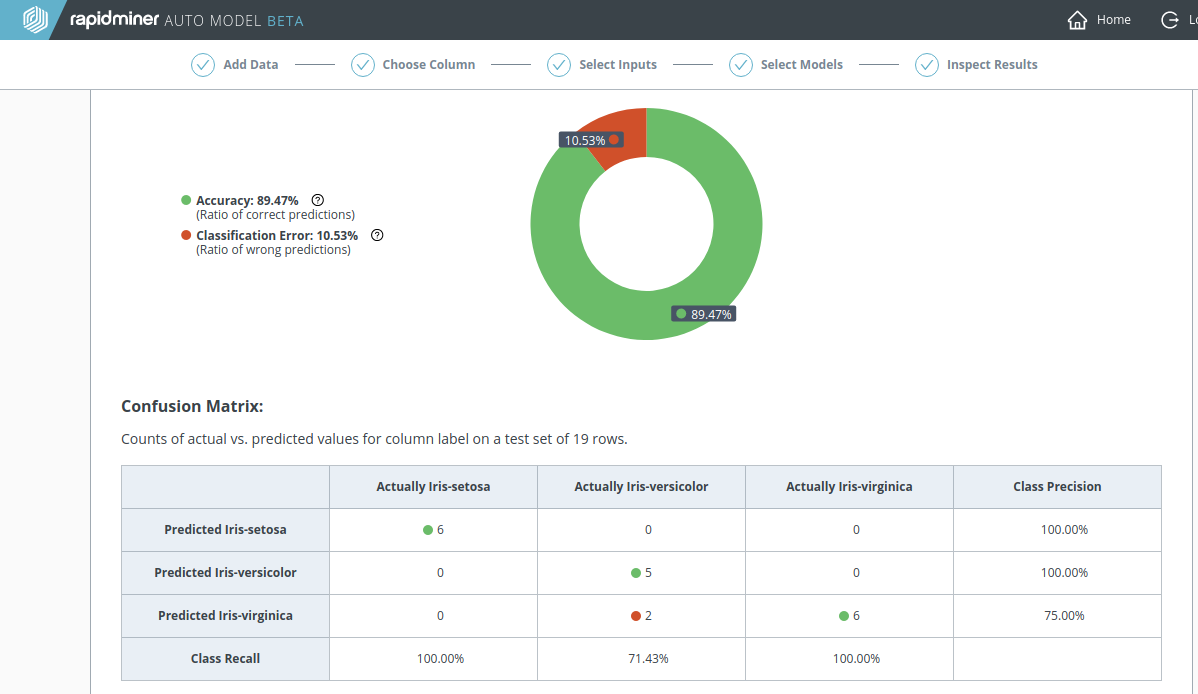
以下の例は、三つの結果を持つ多項分類です。テストデータに適用すると、混同行列内で赤のマークで示されているように、モデルは間違った予測を二つしました。しがたって、二列目の 再現率 は(5/7)で、三行目の 適合率 は(6/8)と100%より少ないです。