回帰
例: 広告データから売り上げの予測に飛びます。
前準備: 平均値 対 中央値
数値のデータセットが与えられたとして、どのように「中心」を決めるといいでしょうか?
この問いへの一般的な答えは、「中心」にaverage(平均値) – meanとも呼ばれます、をとることです。あなたのデータがどのように分布しているかによって、データセットを表す方法として平均が良い場合と良くないときがあります。すべてのデータが密集しているとき、平均は通常とても良い選択です。
データが外側に広がっているとき、データの表し方として、よりふさわしいものがあります。平均値と比べ、median(中央値)は相対的に外れ値の影響を受けにくいです。以下の二つの例を見てください。二つ目のデータセットでは 8 が 108に変わっています。平均値は劇的に変わりますが、中央値は影響を受けていません。
| データセット | {1, 2, 3, 6, 8} | {1, 2, 3, 6, 108} |
|---|---|---|
| 平均値 | 4 | 24 |
| 中央値 | 3 | 3 |
数字を並び替えたとき、 中央値 はデータのちょうど真ん中の数値で、これより小さい値と大きい値の数が同じです。
データを表すのに、平均値か中央値のどちらを選ぶといいでしょうか? 大きな外れ値がなければ問題はないはずですが、二つ目の例のように外れ値がある場合は、調査の目的に応じて決める必要があります。
各データ点が小さな村のある家の世帯収入を表し、他の村とデータを比較したいとしましょう。
- 平均値は村全体の収入(合計)をより正確に表します。
- 中央値は外れ値を無視し、典型的な世帯収入をより正確に表します。
もしあなたがけんかっ早い人であれば、二つ目のデータセットを表すのに平均値も中央値もふさわしくなく、どちらも無視して代わりに全データを図で示すのはどうかとと主張するかもしれません。データが既にある場合は、その主張にいくつかメリットがあります。しかし、(将来の)データはまだ存在していないので、先に予測モデルを構築しています。それほど簡単にこの問題から逃れることはできません。
予測モデルがもっともらしい予測をしない限り、誰もあなたの予測モデルを信じないでしょう。また、予測を行うには現在のデータ( 学習データセット)の中心を定義し織り込む必要があるため、他のモデルより多かれ少なかれ外れ値に注意する必要があります。たとえモデルを作成していなくとも、次の方法で結果をある程度制御できます。
- (a) 適切な評価指標を選択し、
- (b) その指標が最も良いモデルを選択する。
評価指標
いくつか表記を記載します。 N 行の テストデータがあり、行のある一行を n とします。
- Σ_n – テストデータの全行の合計
- Y_n – テストデータのn行目の目的変数の値
- X_n – テストデータのn行目の、Y_nの予測に使用された説明変数の値
- f(X_n) – モデルによって作成された予測。入力としてX_nを用います。Y_n、つまり実際の値と比較します。
実際の値と予測値の差は|Y_n – f(X_n)|と表記され、 residual(残差)とも呼ばれます。もちろん、成功するモデルは残差を最小にすべきですが、残差を組み合わせる方法が複数あるため、様々な評価指標があります。回帰問題の場合、RapidMiner Goは以下の指標を提供しています。
| 評価指標 | 式 |
|---|---|
| Root Mean Square Error (RMSE) | sqrt [ Σ_n (Y_n – f(X_n))2 ] / sqrt(N) |
| Average Absolute Error | (1 / N) Σ_n |Y_n – f(X_n)| |
| Average Relative Error | (1 / N) Σ_n (|Y_n – f(X_n)| / |Y_n|) |
| Squared Correlation (R2) | 決定係数を見てください |
これらの式を言葉に変換しましょう。
| 評価指標 | 概要 |
|---|---|
| Root Mean Square Error (RMSE) | 平均値を好む場合は、Root Mean Square Errorの値が最も小さいモデルを選びましょう。上で説明したように、平均値は外れ値の影響をうけます。 |
| Average Absolute Error | 中央値を好むなら、Average Absolute Errorの値が最も小さいモデルを選びましょう。上で説明したように、中央値は外れ値の影響が小さいです。 |
| Average Relative Error | Average Absolute Errorの変形です。誤差を実際の値のパーセンテージとして計算します。 |
| Squared Correlation (R2) | R2の高い値 (1に近い)を探しましょう。これは予測値と実際の値との間に高い相関があることを示しています。 |
評価指標
予測値 vs 実際の値 の図: テストデータに適用した際、予測値 vs 実際の値のシンプルな散布図は、モデルのパフォーマンスを示しています。データのx座標は実際の値で、データのy座標は予測値です。 y = x の青の実線は、すべての予測が実際の値と等しい理想的な(完璧な)モデルのデータ点の位置を表しています。青の破線は x と y の95%信頼区間の境界線を表しています。データ点が青の実線に近いほど、良いモデルです。
予測誤差の分布 図: 予測誤差(予測と実際の値との差)の頻度ヒストグラムは、テストデータに適用した際のモデルのパフォーマンスを示しています。0の予測誤差は、すべての予測が実際の値と等しい理想的な(完璧な)モデルを表しています。予測誤差が0に近いほど(つまり、0に近い頻度バーが高いほど)、良いモデルです。青の破線は95%信頼区間の境界線を示しています。
例: 広告データから売り上げの予測
回帰分析の例として、 Advertising.csv データセットを調べてみましょう。このデータはGareth James、Daniela Witten、Trevor Hastie、Robert Tibshiraniの著書 An Introduction to Statistical Learningより提供されています。このデータセットの目的は、テレビ、ラジオ、新聞の三つの異なるチャンネル(お察しの通り、これは古いデータセットです)の広告予算の関数として売り上げを予測できると示すことです。
上記のリンクからCSVファイルをダウンロードした後、 モデルの作成で以下のステップに従ってください。
- Advertising.csv をRapidMiner Goへアップロードします
- 予測する列に”Sales”を選択します
- 入力データの一つに”TV”があることを確認してください。テレビ広告は売り上げと高い相関をもっており、予測するのに役立つでしょう。
- すべてのモデルを選択し、実行します。
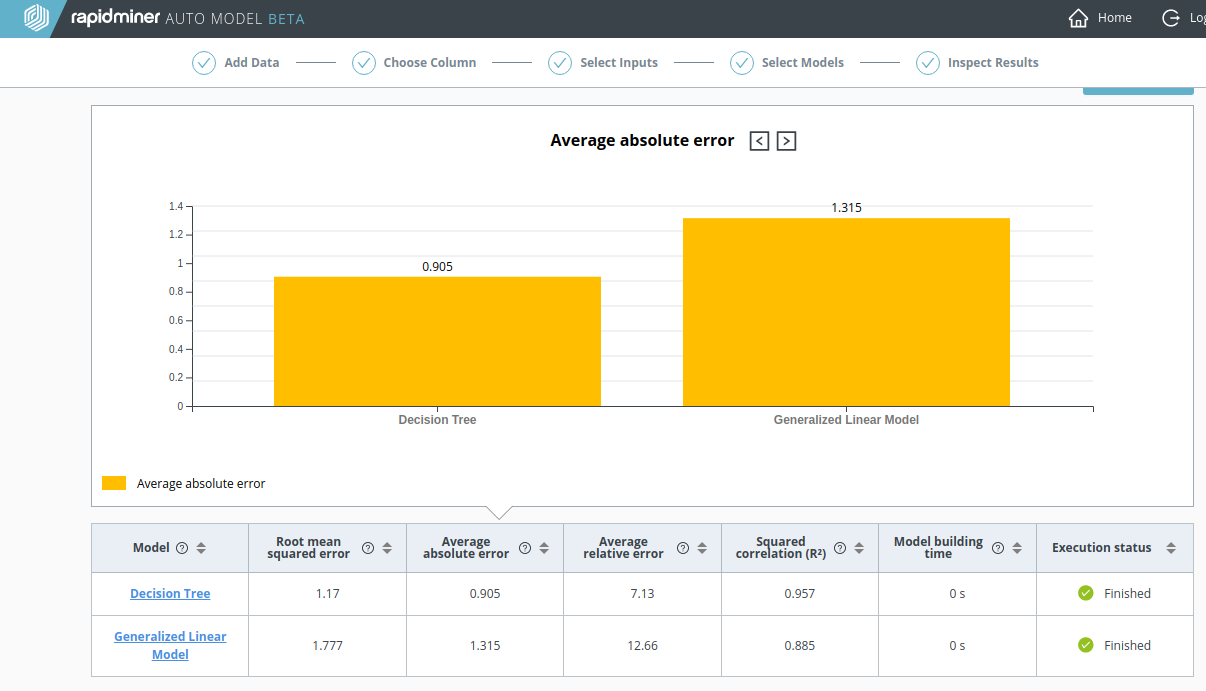
モデルの比較
モデルの比較で、 Generalized Linear Model (GLM)と比較して Decision Tree が勝っていることは明らかです。
- Root mean squared error、 Average absolute error、 Average relative errorの各指標で小さいです。
- 決定係数 (R2)の値も大きいです。
指標間の一致は、このデータセット内に大きな外れ値がないことを示しています。
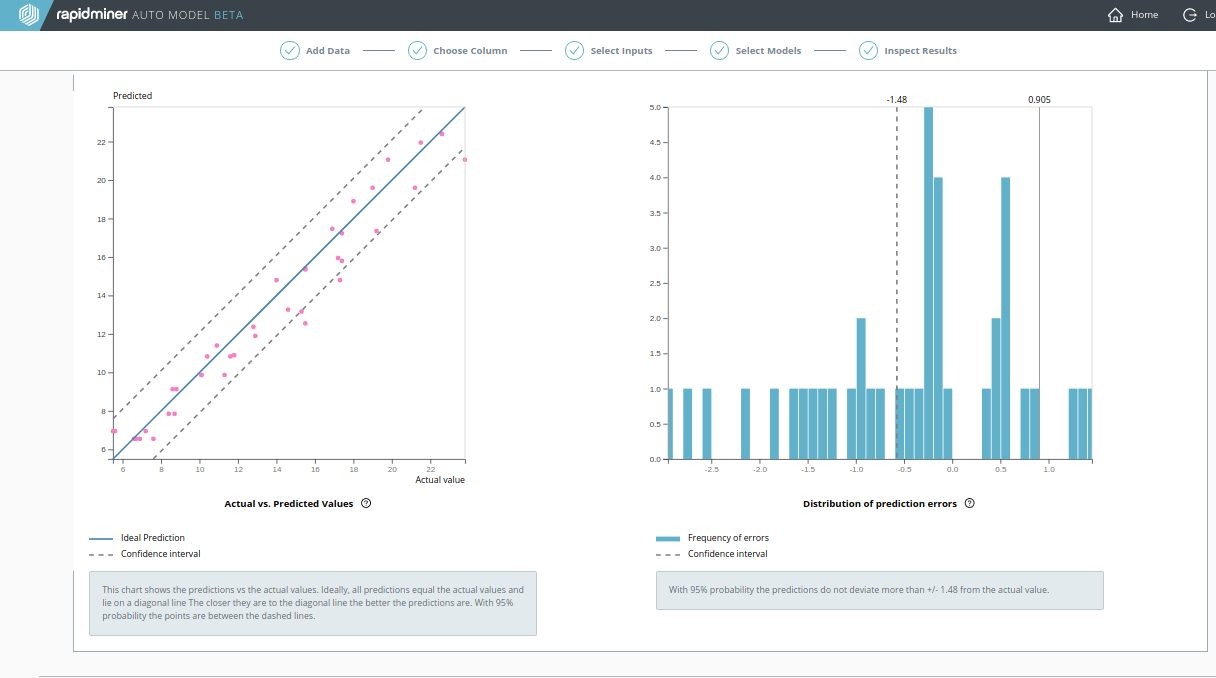
Decision Tree(決定木)
Decision Treeをクリックすると、 実際の値 vs. 予測値 の図を閲覧できます。予測が良いため、直線に似ています。
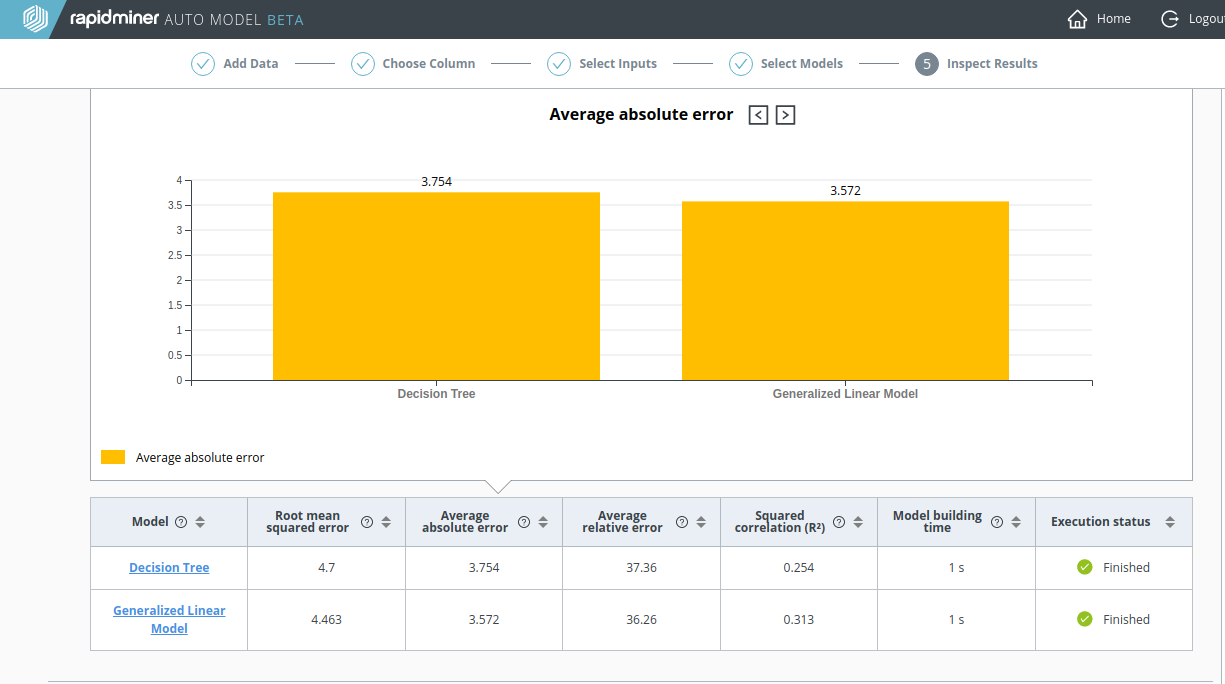
再計算: テレビデータがない場合
Churn Predictive Dataを用いていたときと同様に、高い相関をもつデータが除外されている場合を見てみましょう。以下のスクリーンショットが示しているように、テレビ広告データがないと Decision Tree の結果は非常に悪いです。
- Average Absolute Error は0.905から3.754までと四倍に増えています。
- 決定係数 (R2) は0.954から0.254まで下がっています。
どちらも良くないですが、 Generalized Linear Model (GLM) のパフォーマンスは Decision Treeより良いです。
Decision Tree の 実際の値 vs. 予測値 の図はもはや直線のようには見えません。
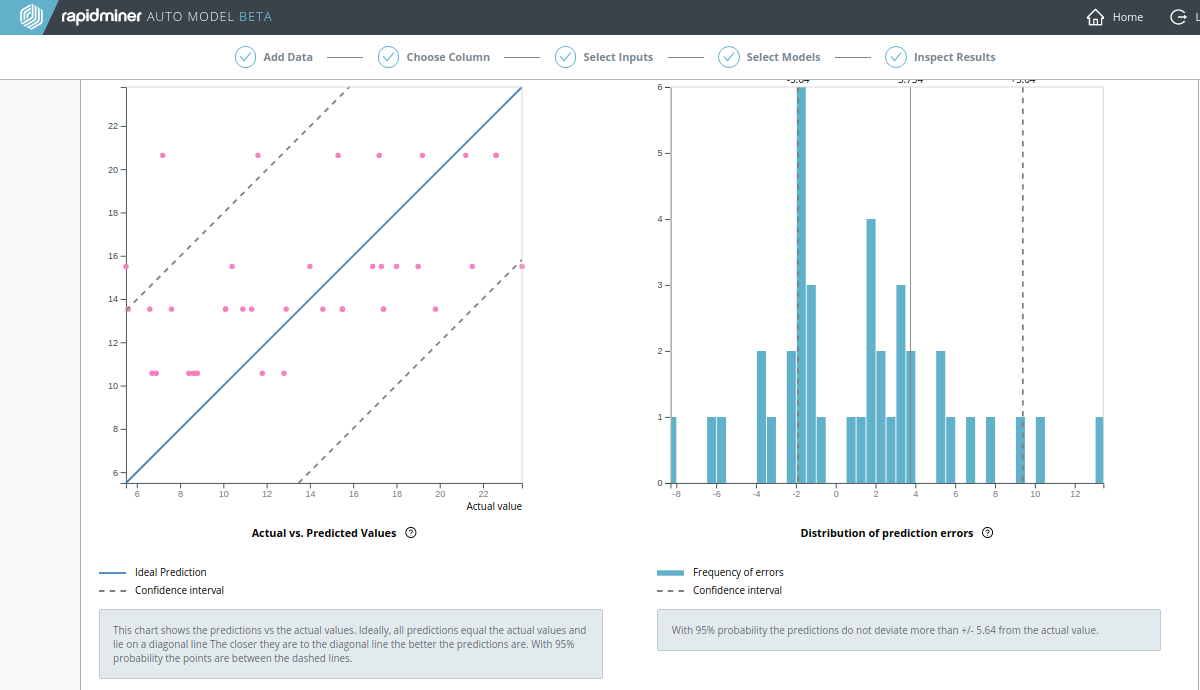
結論? 良い結果を得るためには、すべての関連データが含まれているか確認しましょう。

