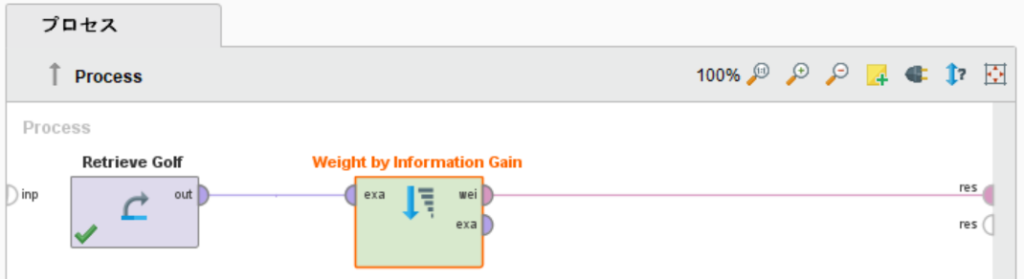
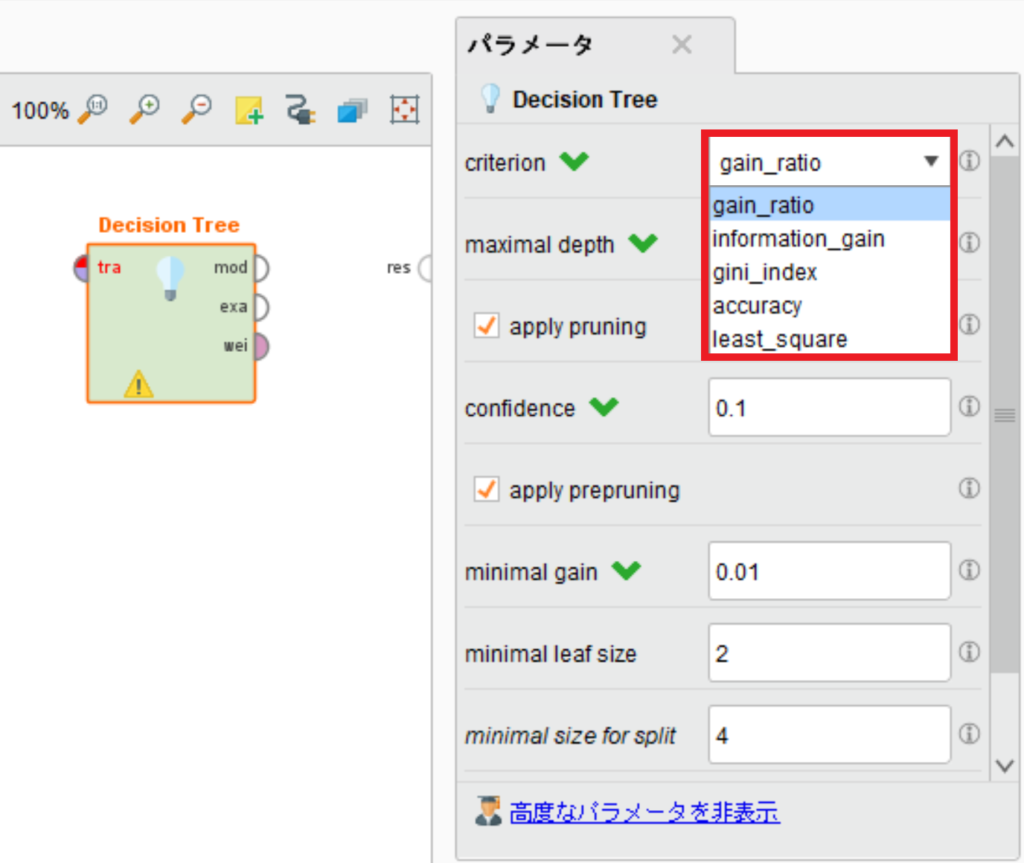
Decision Treeの5種類のcriterion

(回答)
まず最初に、決定木のイメージとして持っていただきたいのは「一番キリの良いところでデータを分ける」ということです。
これらの尺度は、キリの良いところを探すときにどの指標を用いるかが違います。

まず、決定木の主な三つの計算方法についてご説明いたします。
(残り二つについては少々お待ちください。)

①gain_ratio(情報ゲイン比): information_gainの発展形です。情報ゲインを計算したのち、それを分割情報量で割ります。こうして得た情報ゲイン比の大きい属性を分割対象として決定木を作成します。情報ゲイン比にすることでinformation_gainの弱点を克服し、より正常な決定木が作成されやすいです。

②information_gain(情報ゲイン): すべての属性についてエントロピーを計算し、情報ゲインを算出します。そうして情報ゲインのもっとも大きい属性を分割対象として決定木を作成します。ただし、この方法はid属性のような多くの値を持つ属性を選択しやすいという弱点があります。

③gini_index(ジニ係数): すべての属性についてジニ係数を計算し、分割前と比べてよりジニ係数を減らせる属性を分割対象として決定木を作成します。

具体的に、データを使ってご説明いたします。

まずは指標を使わず、データを目で見て決定木を作成してみます。

Samplesの中にあるGolfデータセットを見てください。

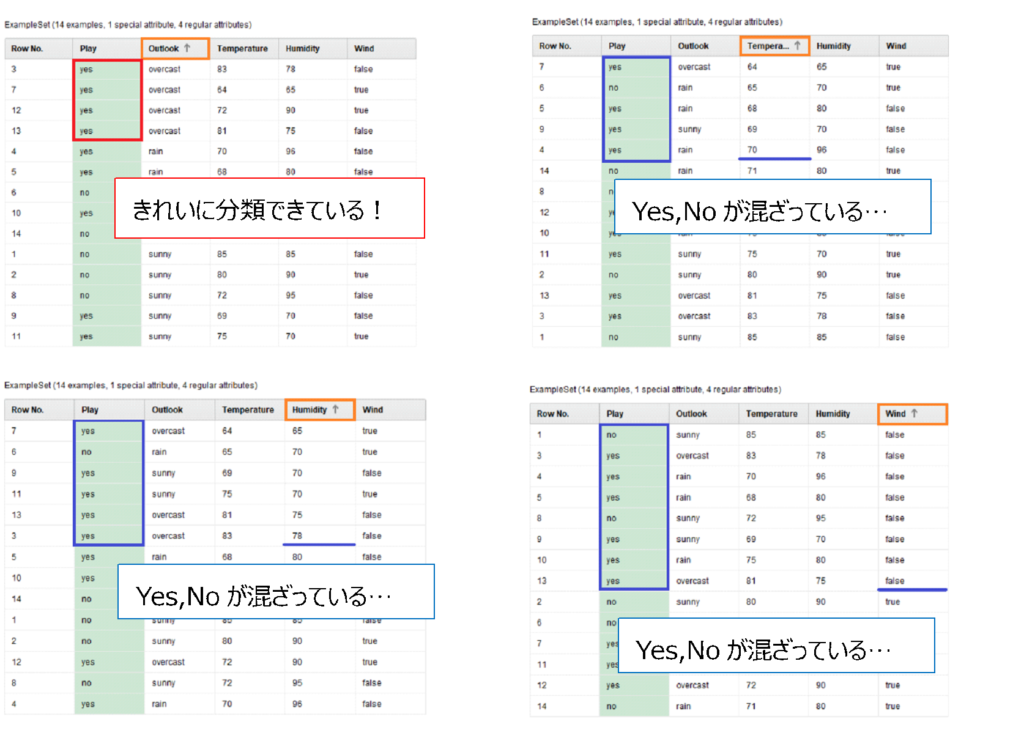
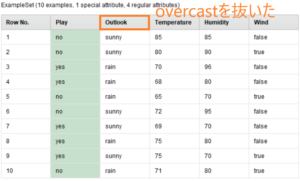
GolfデータセットをOutlook(天気)、Temperature(温度)、Humidity(湿度)、Wind(風)の順に並び替えてみます(下図)。

その並び替えた中で、一番キリの良いところで分けられるのがOutlook=overcastです。

Outlookで分けると、overcast(曇り)のときに目的変数Playが全てyesになり、きれいに分けることができています。ほかのTemperature、Humidity、Windでも分けてみましたが、どうしてもyesとnoが混ざってしまっています(Temperature、Humidityに関しては数値なので、一番分けられそうなところで分割しています)。

そのため、一番キリの良いところで分けられるOutlookでまずはデータを分けます。

データをOutlook=overcastで分けた後、以下のようなデータが残ります。

この残ったデータからさらにキリの良いところで分けられる部分を探していきます。

試行錯誤した結果、Outlook=rainとOutlook=sunnyに分けてみます。

すると、rainのほうはWindで、sunnyのほうはHumidityで上手く分けられそうです。
ゆえに、以下のような決定木を得ることができます。

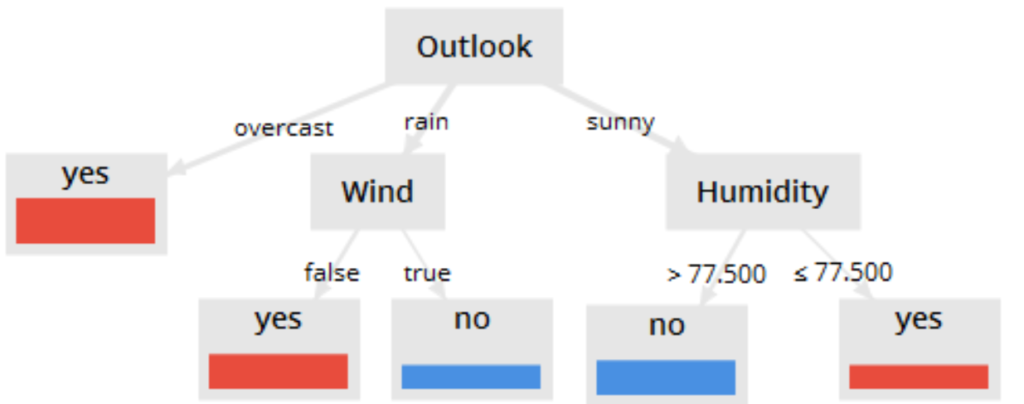
今、上記の例では一つ一つデータを目で見てPlayのyesとnoに分けられるかを見てきましたが、常に目で見るのは大変です。

そこで、どれくらい上手く分けられているかを数値で表します。この数値を不純度と言い、不純度の指標にエントロピーとジニ係数の主に二種類があります。

エントロピーを用いて木を作成するものが②information_gain、
ジニ係数を用いて木を作成するものが③gini_indexになります。
①Gain_ratioは②information_gainの弱点を克服したもので、発展形にあたります。
そのため、説明も②information_gainからさせて頂きます。

②information_gain
Information_gainは不純度の指標にエントロピーを用いて木を作成していきます。
エントロピーはデータの混沌性を表し、エントロピーが低いほど整理されていることになります。
つまり、整理されている部屋はエントロピーが低く、散らかっている部屋はエントロピーが高くなります。
決定木の場合はデータがまとまっているほうが望ましいので、エントロピーは低いほうが良いです。

エントロピーは、以下のように計算されます。

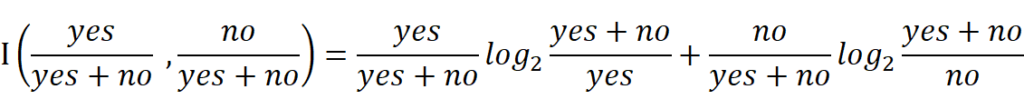
つまり、最初の何も分岐していないGolfデータセットについて、yes=9、no=5のエントロピーは

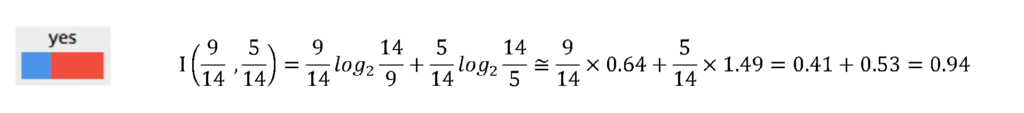
まだ何も分類していないだけあって、今の状態は混沌としているようですね。
なお、どちらかに固まる場合(yes=14,no=0のような時)、エントロピーは0になります。
逆に半々になる場合(yes=7,no=7のような時)、エントロピーは1になります。

ここから場合分けし、エントロピーが最も低くなる属性でデータを分割します。

Outlookについて分けた場合のそれぞれエントロピーを計算し、それにデータ数比をかけます。
データ数比をかけたあと、元の何も分割していないもの(上記の0.94)との差を求めます。
これを情報ゲインと言います。

Outlookについて見たので、Windで分割した場合・Temperatreの場合・Humidityの場合について見ていきます。
(Temperatureについては省略しています。)

ゆえに、最も情報ゲインが大きいOutlookで最初は分けられます。
情報ゲインが大きいということは、その属性で分割した場合のエントロピーが低いということです。そのため、情報ゲインの大きい属性を選択します。
Windの情報ゲイン、Temperatureの情報ゲイン、Humidityの情報ゲインと比べていき、最も大きな情報ゲインになったものを採用していきます。これがinformation_gainです。
ただし、information_gainには弱点があるので、それを克服したgain_ratioについて次は見ていきます。

①gain_ratio
順番が前後してしまいますが、gain_ratioについて説明いたします。
実は、先ほど見たinformation_gainには枝分かれの多い属性を選んでしまうかもしれない、という弱点があります。

例えばid番号で枝分かれする、のようなものをイメージしてください。
Id番号で枝分かれしたとき、決定木としては正しくないですが、エントロピーは低くなってしまうのです。

これを解決したものがgain_ratioです。
Gain_ratioは情報ゲインを分割情報量で割ったものです。
分割情報量は以下で計算したものの総和です。

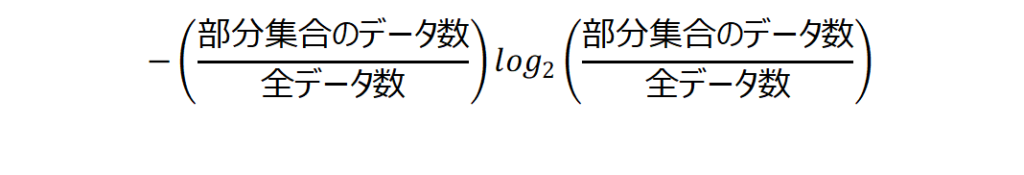
最初の分割にOutlookで分けた場合で見ていきます。
例えば、先ほど計算したOutlookの情報ゲインは0.25でした。

同様にWind,Temperature,Humidityについて計算していき、情報ゲイン比の最も大きい属性で分割します。

③gini_indexについて
ジニ係数もエントロピーと同様に、不純度を表す指標です。ジニ係数が低いほうが整理されたデータです。
そのため、ジニ係数が小さいほうが決定木にとっては望ましいです。
ジニ係数は次のような式で計算されます。

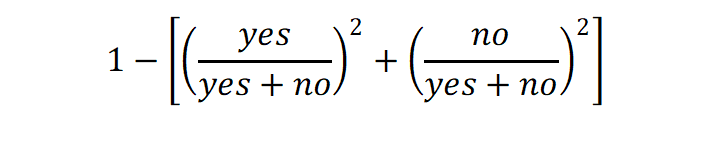
最初の状態だと、ジニ係数は

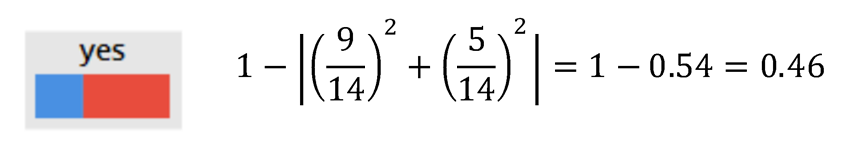
Outlookで分割した場合、

ゆえに、0.12不純度を減らすことができました。
そのため、分割する際はこの差が最も大きいものを選ぶことになります。

今、Outlookについて見たので、次はWind・Temperature・Humidityについて見ていきます。
(Temperatureは省略しています。)

ゆえに、ジニ係数で計算した場合も、最初はOutlookを選ぶことになります。
このように一つ一つ計算して木を成長させていきます。

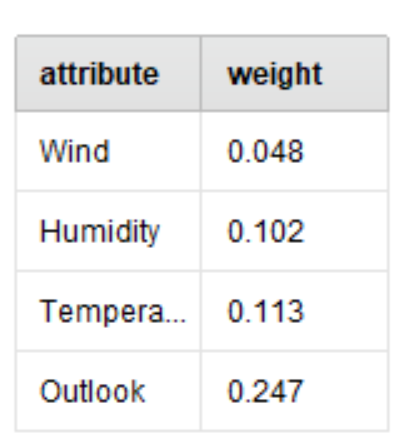
なお、今は手計算で算出してきましたが、Weight by Information GainやWeight by Gini indexなどのオペレータを使うと自動で情報ゲインなどを算出してくれるのでご活用ください。
(このとき、情報ゲインなどは小数点第三位まで計算されています。)