ROC曲線

(回答)

Performanceオペレータなどを用いた際、結果画面に表れる図は「ROC曲線」と言って、作成したモデルが良いのか悪いのかを表しています。
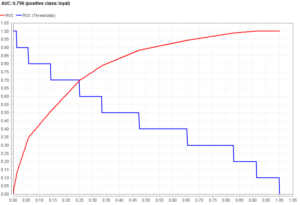
まずは真ん中の図(AUC(何もなし))からご説明いたします。

訓練データにGolfデータ、テストデータにGolf-Testset、使用するアルゴリズムにk-NNを用いて詳しく見ていきます。
k-NNのkを3にし、weighted voteのチェックを外してください。

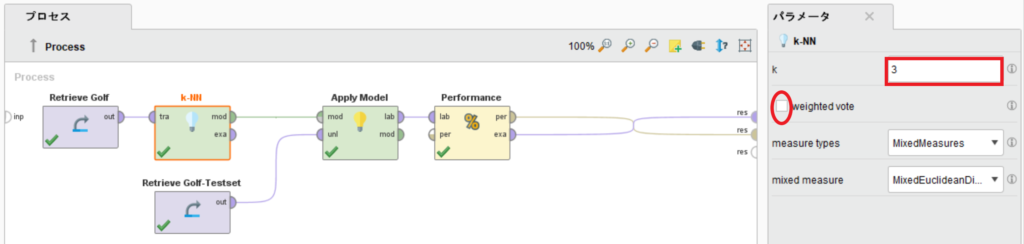
このプロセスを実行した結果、以下のような混合行列とデータが得られます。

混合行列より、真陽性率と偽陽性率というのを算出します。
真陽性率(=再現率;recall)= TP/(TP+FN)=8/(8+1)=0.88
偽陽性率= FP/(FP+TN)=4/(4+1)=0.8
真陽性率は再現率(recall)と同義で、yesのうち、どれだけ予測を当てられたかの割合です。
偽陽性率はnoのうち、間違えてyesと予測してしまった割合です。つまり1からnoのrecallを引いた値と同じです(1-0.2=0.8)。

一方、出力されたデータを見てください。
デフォルトでは、Confidence(yes)の値が0.5以上だとyesと予測されます。

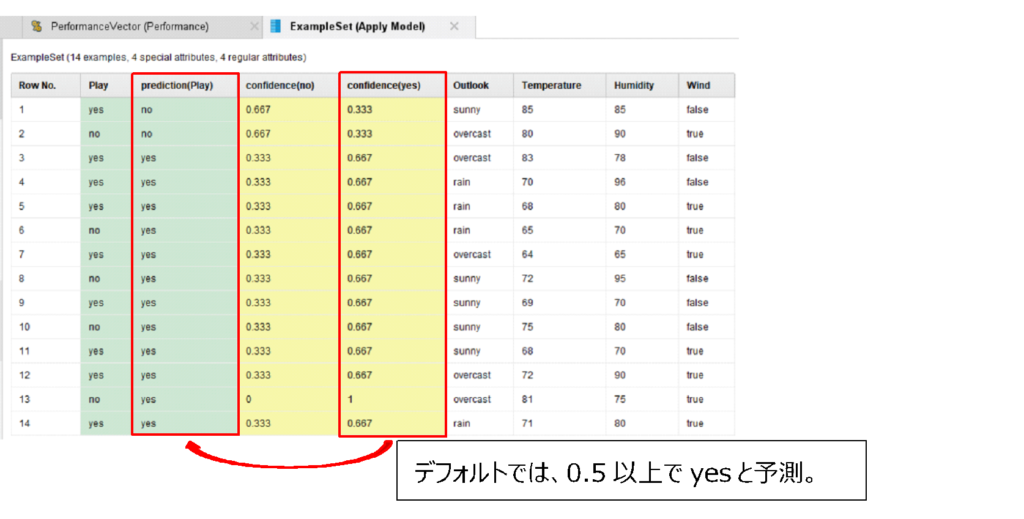
ROC曲線は、このconfidence(yes)の値を、どこからyesと判断するか(閾値と言います)を変えて、x軸に偽陽性率、y軸に真陽性率をプロットした図になります。

つまり、今は閾値が0.667のとき、真陽性率0.88、偽陽性率0.8なので、(0.8,0.88)にプロットされます。
閾値が0.667になっているのは、0.333、0.667、1でyesかどうかが変わるためです。

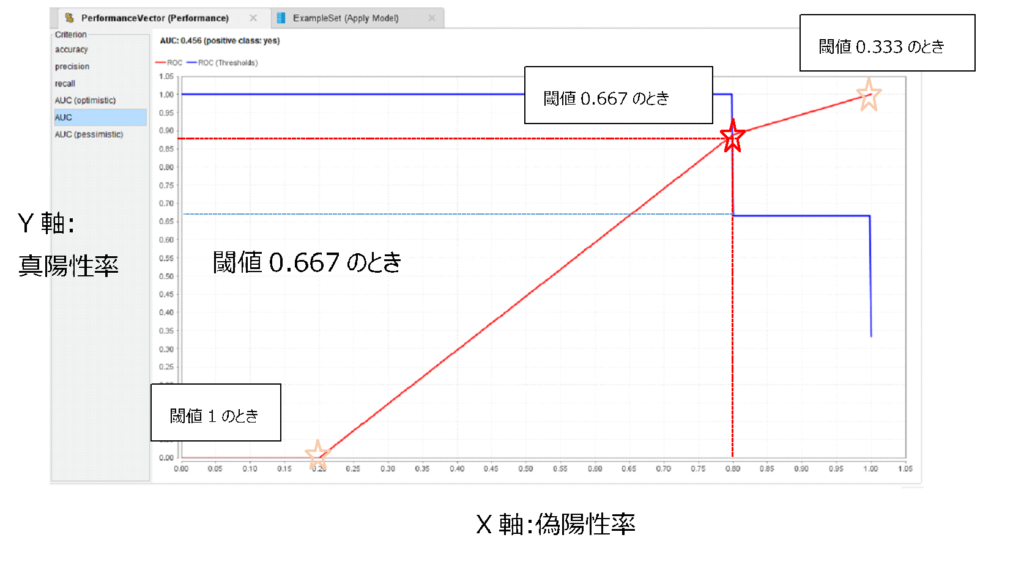
これが、閾値0.333のときと1のときについても見て、プロットします(図のオレンジの星)。
計算は以下のようです。
閾値1(confidence(yes)>=1) のときの混合行列

真陽性率(=再現率;recall)= TP/(TP+FN)=0/(0+9)=0
偽陽性率= FP/(FP+TN)=1/(1+4)=0.2
閾値1のとき、(0.2,0)にプロットする

閾値0.333(Confidence(yes)>= 0.333)のときの混合行列

真陽性率(=再現率;recall)= TP/(TP+FN)=9/(9+0)=1
偽陽性率= FP/(FP+TN)=5/(5+0)=1
閾値0.333のとき、(1,1)にプロットする
そのプロットしたものを線上につなげたものがROC曲線です。

ROC曲線は、左上にいくほど良いモデルです。

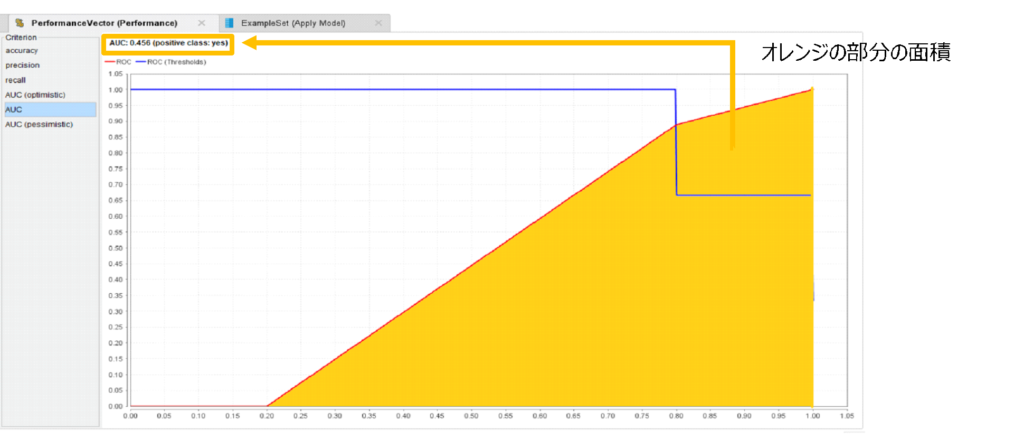
ですが、複数のROC曲線があるとして、それを目で判断するのは大変なので、ROC曲線の下の部分の面積を出します。
それがAUC(area under the curve)です。
AUCはROC曲線の下の部分の面積なので、1(底辺)×1(高さ)=1より、最大1になります。
そのため、AUCは1に近いほうが良いモデルになります。
今回のAUCは0.456と0.5以下なので、良いモデルではありません。おそらく、データが少なすぎるのでしょう。

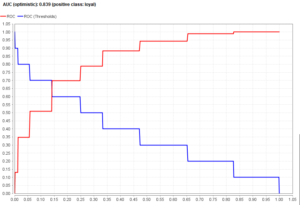
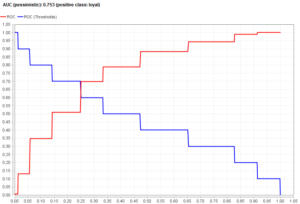
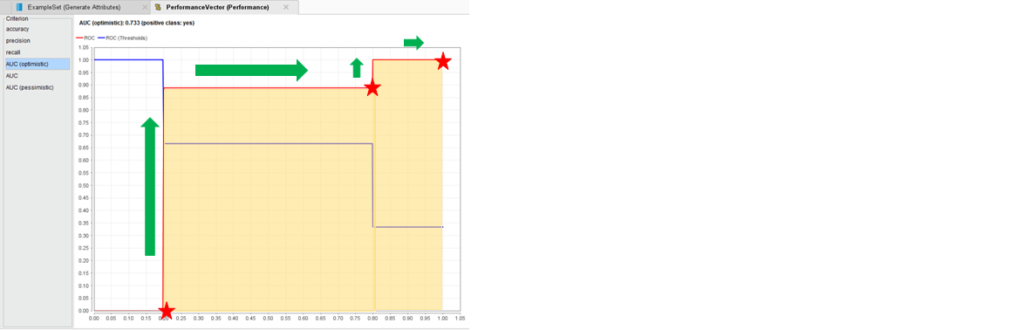
次に、AUC(optimistic)とAUC(pessimistic)について見ていきます。

AUC(optimistic)とAUC(pessimistic)の違いは、 x軸に偽陽性率、y軸に真陽性率をプロットした後、線上にする際に上から行くか右から行くかの違いです。

AUC(optimistic)の場合、

AUC(pessimistic)の場合、

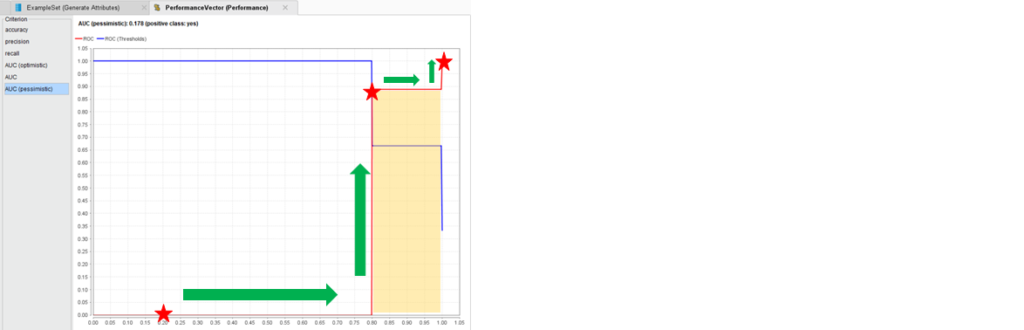
このように、線の繋げ方でAUCが変わるため、optimisticとpessimisticの二つがあります。
このAUCの値の変化が見られるようにoptimisticとpessimisticの画面があります。
なお、直線で繋いだものがAUC(何もなし)になり、ちょうどoptimisticとpessimisticのAUCの平均と同じです。